DESCRIPTION

v.voronoi uses an existing vector points map (input) to create a Voronoi diagram (Thiessen polygons) in a new vector map (output).

The bounds of the output map are limited by the current region. (see g.region)


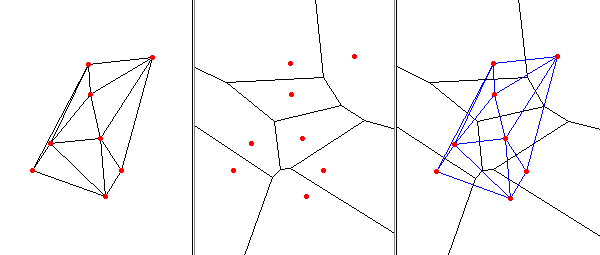
Voronoi diagram and Delaunay triangulation example:


Delaunay Triangulation (left pane), Voronoi diagram (center pane), and both (right pane)

NOTES

Voronoi diagrams may be used for nearest-neighbor flood filling. Give the centroids attributes (start with v.db.addcol), then optionally convert to a raster map with v.to.rast.

EXAMPLE

Commands used with the Spearfish dataset to create the above figure. 
  g.region n=4927250 s=4919400 w=588650 e=594850
  d.frame -c fr=one at=0,100,0,33.3333
  d.frame -c fr=two at=0,100,33.3333,66.6667
  d.frame -c fr=three at=0,100,66.6667,100

  v.delaunay -lr in=archsites out=arch_delaunay
  d.frame -s one
  d.vect arch_delaunay
  d.vect archsites color=red fcolor=red size=5 icon=basic/circle

  v.voronoi -l in=archsites out=arch_voronoi
  d.frame -s two
  d.vect arch_voronoi type=line
  d.vect archsites color=red fcolor=red size=5 icon=basic/circle

  d.frame -s three
  d.vect arch_voronoi type=line
  d.vect arch_delaunay color=blue
  d.vect archsites color=red fcolor=red size=5 icon=basic/circle

BUGS

Only attribute table of field 1 is copied.

REFERENCES

Steve J. Fortune, (1987). A Sweepline Algorithm for Voronoi Diagrams, Algorithmica 2, 153-174.

SEE ALSO

g.region, v.delaunay, v.hull

AUTHORS

James Darrell McCauley, Purdue University
GRASS 5 update, improvements: Andrea Aime, Modena, Italy
GRASS 5.7 update: Radim Blazek

Last changed: $Date$